Summary:

Our information theoretic model with feedback presented at SMC 2018 is extended. We tackle the description of complete trajectories and incorporate a feedback mechanism. We find a characterization on the speed at which variability is reduced throughout the movement. This decrease explains Fitts’ law, and more generally, the speed-accuracy tradeoff.

Contrary to many previous works, we tackle a set of synchronized trajectories, rather than single trajectory. Here is an exemple of a set of synchronized trajectories performed under identical conditions

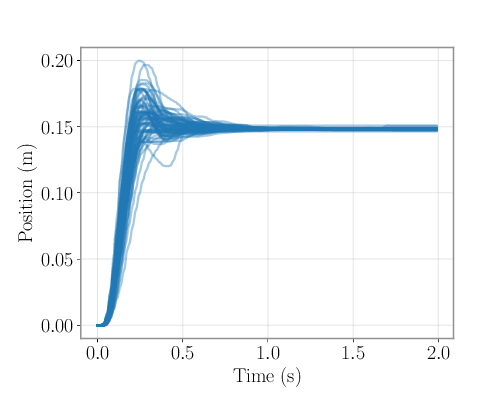
We were interested at characterizing the variance of this set of trajectories, and how it evolved over time. Indeed, our hypothesis was that when performing precise movements, moving the limb is not what takes the most time (this is clear from the previous figure, where you see that the target is reached on average in about 250ms, but movements last up to 1s).

We obtained typical profiles like the one displayed below (in log-lin scale)

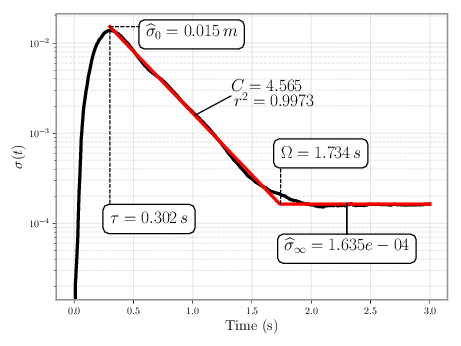
What we see if that the variance profile can be described by two phases:

• A first, short phase, where variance increase rapidly
• A second, much longer phase, where variance reduces gradually.

In this example, the reduction in variance is seemingly linear, with a slope -C (considering the plot is in log-lin space, there is thus an exponential reduction of variance). This is something we had predicted theoretically. We were also able to link C to 1/b in Fitts’ law. Another notable fact is that the first phase can be approximated to be of constant duration, on the data that we observed.

The following figure summarizes nicely those results. Participants were asked to perform movements under 5 conditions (from extremely precise to extremely rapid).

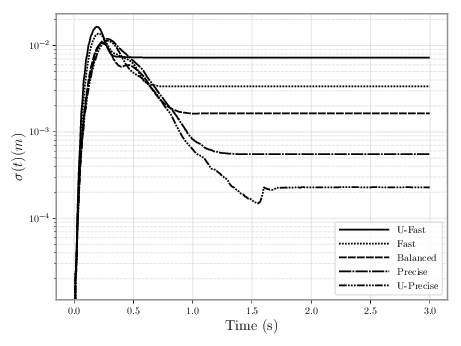
We see that the maximum variance point is approximately always at the same point in time (almost constant first phase), that the curves have about the same slope (exponential decrease of standard deviation at a rate that is constant through all 5 conditions). As a result, the only way to increase accuracy of a movement is to spend more time during the second phase, which explains the speed-accuracy tradeoff. You can see this as the conditions with higher precision requirements level-off later in time. Finally, we also recovered Fitts’ law, in both its effective and nominal versions.

Find out more by reading our paper!